To the newly initiated, learning about how Torus works can feel like information overload. We’ve written about the Torus Network at a high level in our docs, but in this series, we’ll dive a bit deeper into the fundamentals of how it all works, and the ideas that make Torus possible. How is the distributed key generation (DKG) implemented? How are key shares migrated across nodes? Why do we even need to migrate shares? In this series, we will cover the core intuitions of each of these concepts, ELI5-style.
Private keys on the Torus Network are stored as shares. These shares follow a threshold access structure — as long as you have more than half of the total shares, you can recover your private key. For example, if there are 3 shares in total, you would need at least 2 of the shares to recover your private key. Threshold secret sharing schemes like this have been around since the 70s, and the most basic threshold secret sharing scheme is Shamir’s Secret Sharing.
Shamir’s Secret Sharing
To briefly recap public and private keys, elliptic public-private key pairs are what we use to interact with the different blockchains, with the most popular variants being Secp256k1 (used by Bitcoin, Ethereum among others) and ED25519 (used by newer chains like Solana, Near, Libra, Tendermint). Vitalik has a great series on that and how elliptic curves work, but for now, you can treat the private key as a number, and public key as a function on that number.
The fundamental concept that most DKGs are built on is called Shamir’s Secret Sharing. And while the paper might be confusing to read, the underlying intuition is simple:
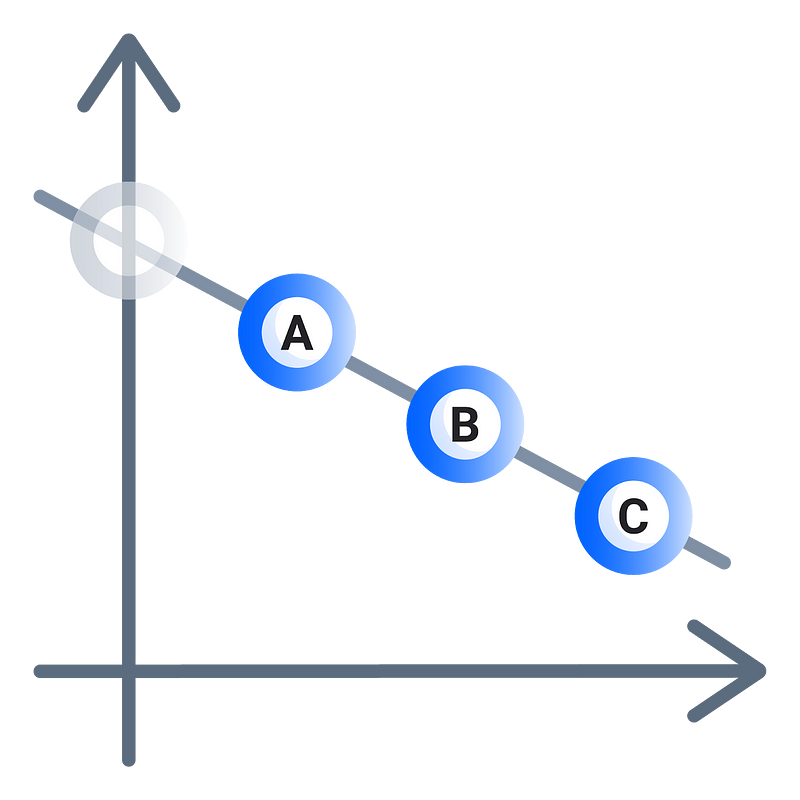
Imagine drawing a line on a graph, with a secret at the y-intercept. Now, you give out shares to 3 different people — A, B, and C. You now erase this line and challenge these three people to reconstruct the line you have erased.
In order to reconstruct the line, one person’s point is not enough — at least two points are needed to reconstruct the line. This is 2-out-of-3 Shamir Secret Sharing.
As you can imagine, this is also extensible for higher powers of x, so a quadratic curve requires three points and a cubic curve requires four.
These points (shares) are held by the nodes on Torus Network. When you authenticate with them via a login, you retrieve these points and reconstruct your key in front-end client of your browser.
Share distribution & Verifiable Secret Sharing
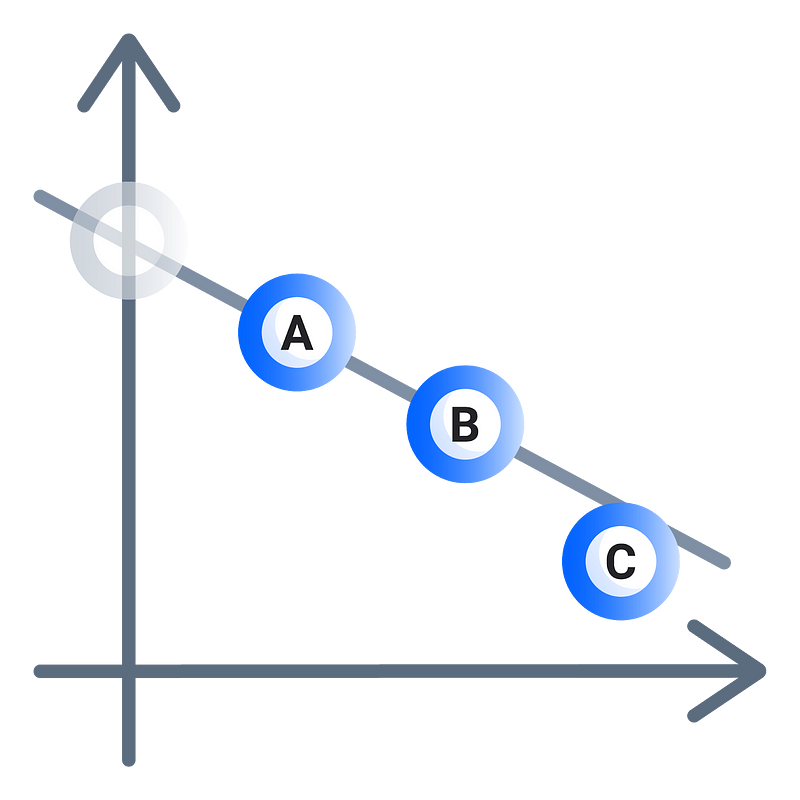
Shamir Secret Sharing has several shortcomings. One of the problems is that it is not possible for share-recipients to know if the shares they have are consistent with the shares that other people have received. For example, Dealer Dennis wants to distribute shares to his best friends Alice, Bob and Charlie, however, unknowing to anyone else, Dennis secretly dislikes Charlie. Dennis gives Bob and Alice their shares but issues Charlie a wrong share.
In this scenario when Dennis requests for his shares back, Alice and Bob cannot tell if Charlie is lying, or if the dealer, Dennis, is malicious. Alice and Bob present their shares, but Charlie can’t because he never received them. He is now outcasted by the group — poor Charlie. This problem is solved by using Verifiable Secret Sharing (VSS) schemes. Verifiable Secret Sharing is a way to distribute shares that allows Alice and Bob to be reassured that Charlie has a share.
Instead of Alice simply giving out her shares to Bob, Charlie, and Dennis separately, Alice makes commitments to the coefficients of the line, which can be independently verified by the recipients. This allows recipients who have received a wrong share to issue complaints, which must be answered by the dealer. Failure to answer complaints results in the dealer being omitted from the secret-sharing protocol. Moreover, in some cases, this also means that a timeout may be necessary to ensure that the dealer has enough time to respond to complaints.
Torus uses a variant of VSS called Asynchronous Verifiable Secret Sharing (AVSS), that uses bivariate polynomials to handle this complaint phase (at the cost of message size), and achieves successful secret sharing under asynchronous network assumptions (no timeouts).
Distributed Key Generation
At this point, we know how to share our key such that all participants receive them, but we still have a problem — there still exists a dealer who knows the initial secret. In the first diagram, when you drew the line, you were aware of the secret (y-intercept)! Using a system like this would make Torus keys very insecure since nodes would be aware of your private key at some point.
This problem can be solved by having every single person involved do a secret sharing, and summing up the shares of these secret sharings — this is the basis of Distributed Key Generation.
The way DKGs do this is through allowing each node operator to contribute to the overall randomness of the key. The protocol starts off with basically conducting n independent runs of AVSS, where n is the number of nodes in the network.
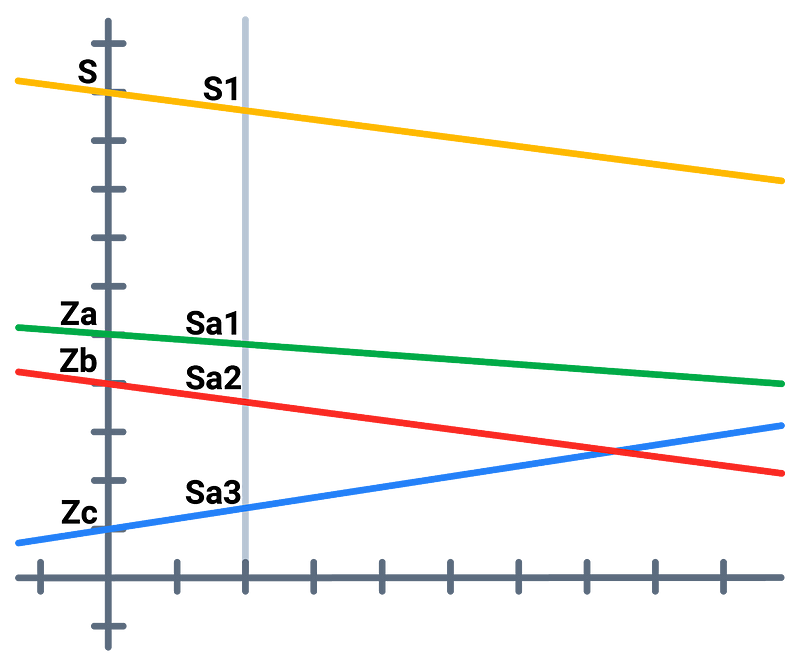
If Alice, Bob and Charlie ran nodes, each of them would first create a random secret (Za, Zb, Zc) and distribute its shares across the network. This results in each of the node operators having three shares — Alice has one from the key she generated herself, and one respective to each of the other nodes (in total, she has Sa1, Sa2, Sa3).
The final line (in yellow) that we will be using for secret sharing is the sum of all of the three lines from Alice, Bob and Charlie, which has a secret S = Za + Zb + Zc
Similarly, when Alice sums up the shares that she has, she acquires the final share (S1) respective to the master public-private key pair, which she can then use with Bob’s S2 or Charlie’s S3 to reconstruct the S.
Since no single node knows all of the secrets Za, Zb, and Zc, and the yellow line was never physically constructed, it’s not possible for a single dealer to know the user’s private key,
The distributed key generation protocol has 3 rounds of communication, so it can take some time to create a key. Torus nodes conduct the key generation in parallel for multiple keys and hold a buffer of them as an optimization, to ensure sub-second response times for new users.
Read Part 2: Key Assignments, Resolution and Retrieval
Stay Tuned for Updates
Join our community for updates on the progression of Torus and drop us a line on any of our social channels if you’d be keen on joining us bring blockchain adoption to the mainstream.





