Shamir’s Secret Sharing (SSS) vs. Threshold Signature Scheme (TSS) Explained

We are sharing a detailed comparison of how Shamir's Secret Sharing works versus Threshold Secret Sharing and how they apply to WaaS solutions.

If we are only talking about user experience, then it is easy to find a working cryptographic solution that will abstract the task of securing and recalling private keys for a regular user. The most common of them is splitting the key during distributed key generation (DKG), bringing it among several places like the user’s social logins and biometrics, and then generating signatures from these fragments.

But how does it actually happen?

One of the more popular schemes to do this is Shamir’s Secret Sharing– known for its flexibility and ready-made availability to anyone who would want to implement it. Many Wallet-as-a-Service (WaaS) solutions are using SSS as a signature scheme, however, SSS comes with its risks that, if not set up correctly, may allow users' keys to be exposed to attackers.

Another solution we have is Threshold Signature Schemes (TSS)– a cryptographic mechanism that will allow multiple parties to create a partial signature that will then be aggregated to sign a transaction.

But what’s the difference between the two, and how do they work in key management in WaaS? 

Consider this scenario…

A wallet is managed by three devices holding a fragment of the key each in a 2/3 threshold. This means that to successfully sign transactions with the wallet, a quorum of at least two of the devices must be established. How do you prevent all of these devices, as well as any external party, from knowing the complete secret signing key?

How does Shamir’s Secret Sharing Work?

Shamir's Secret Sharing can somewhat help solve this problem. It allows a secret key to be divided into multiple shares and reaching a minimum threshold of these shares will reconstruct the original secret. The algorithm relies on polynomial interpolation to generate the shares based on points on a polynomial curve, which makes it very flexible as you can infinitely extend the number of devices that hold a share without breaking the setup.

The Limitations of SSS

There are many SSS solutions that developers can use out-of-the-box. However, this could lead to vulnerabilities when implemented incorrectly. For instance:

• If the private key is generated in a DKG protocol and was distributed using SSS, the key will be reconstructed and can get exposed upon reconstruction. In the same way, if the environment is unsecure, it can also be exposed everytime the wallet signs a transaction because the whole of the key is stored temporarily to create the signature. 
• There is also the risk of maliciously changing some of the shares. SSS is only made to create the key if the minimum quorum is reached, but it has no way to verify that ALL shares that have been sent are correct. And this means that a corrupted dealer can send malicious key shares and still have the key reconstructed, and this action may lead to them gaining information from the shares submitted by the honest participants.

Verifiable Secret Sharing (VSS) was used as an extension of SSS to remedy this, and it adds a verification step before key reconstruction. However, the key is still stored as a whole after reconstruction so the risk of stealing the key remains.

Now we start to see why using SSS and VSS in extension can be dangerous if used in the wrong places. While it is an excellent method for dividing secrets, it falls short when it comes to providing the security guarantees needed to reduce attack opportunities for parties who intend to steal the keys. In Web3Auth, we have used a specialized node infrastructure as an entry point to retrieve the private key in SSS, making sure that the key can only be accessed by an authorized device.

Key Storage and SSS

There are two ways to store the keys and their shares in combination with SSS: first is using a centralized Key Management System (KMS), and second is using Multi-Party Computation (MPC).

KMS stores the encrypted key in cloud servers that are controlled by the platform. When used with SSS, it temporarily stores the reconstructed key on these servers. This makes for a fast and convenient solution but it also makes the wallet non-custodial and the reconstructed key even more vulnerable.

MPC protocols on the other hand employ various parties to have the key shares computed in a privacy-preserving manner once a quorum is reached. It sometimes uses SSS as a mechanism to store and retrieve the whole private key. But as with KMS, it still relies on storing the whole reconstructed key to generate the signature, but this time just in the user’s device, which is a little more secure than KMS.

Key Management with Threshold Signature Schemes

So, considering the main problem with SSS which is having the full key temporarily stored after reconstruction, what can be another way to generate digital signatures with multiple parties?

Threshold Signature Schemes (TSS) is a way for participants to sign messages with only their shares by allowing the partial keys to be constructed in parallel. These partial keys are then aggregated via Lagrange interpolation, validating the final signature without ever reconstructing it. It resolves many of vulnerabilities in SSS, mainly:

1. No Single Point of Failure

Because parties can create partial signatures simultaneously, it creates the signature without the full key ever being reconstructed or stored in a single place, leaving zero chance for any bad actor to steal them. 

2. Verifiability of Key Shares

TSS also adopts a verification step like in VSS to prevent corrupt participants from altering their key share, and it also uses polynomial interpolation but this time with the verification running in parallel, and with mechanisms that enable one party to construct their part of the aggregated signature without knowing anything else about the inputs of the others.

3. Flexibility in Number of Participants

The number of signers from the signature generation phase can be adjusted when TSS is used with Proactive Secret Sharing, so it also offers the flexibility to add new participants or revoke a share from an existing threshold group, much like in SSS. 

Web3Auth’s MPC-TSS Solution

With the Web3Auth MPC-TSS infrastructure, users’ key is divided into multiple parts and stored across users’ devices and our Auth Network. This ensures that users’ key is always available and never stored in a single place.

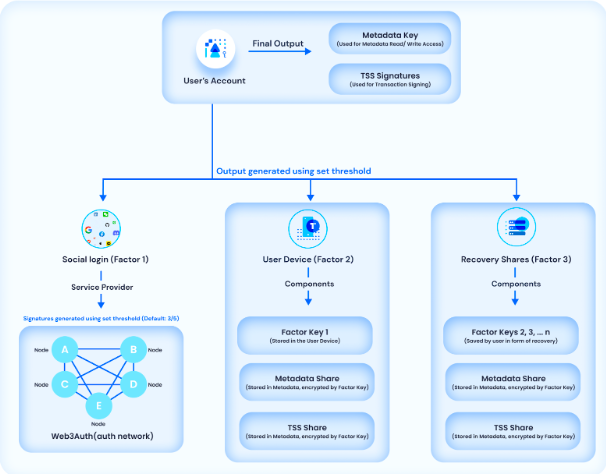
By using TSS, Web3Auth wallets are therefore able to generate the signature without needing to combine the key shares, making it a secure key management infrastructure all while maintaining SSS-like flexibility.

Conclusion

While Shamir's Secret Sharing is a valuable algorithm for dividing secrets, it should be used with caution and be provided a secure environment. Its main weak points are its lack of verifiability for inputs and its need to reconstruct and store the key to be able to sign a transaction.

This can be solved by a different cryptographic approach called Threshold Signature Scheme (TSS) which uses distributed computation to generate the signature, never needing to create the full key while ensuring the integrity and robustness of the signature generation process. 

FAQ:

Where can I find more information about how Web3Auth implements Threshold Signature Schemes?

To know more about Web3Auth’s MPC Architecture, please refer to this article in our documentation.

Which types of TSS does Web3Auth support?

We support the popular GG19, GG20, EDDSA, and DKLS19, in result supporting the ecdsa signature standard on both elliptic curves. We are also agnostic to TSS implementations so we support other signature schemes like EDDSA or its Schnorr variants, BLS, and Stark (coming soon)

I need to implement a TSS that is not on the list, who can I ask for customizations?

Our team is open to requests for specific elliptic curve/chain support, please feel free to join our monthly community gathering, or set up a call with the team.